题意:

225

给你一个数字串,求有多少个子序列是3的倍数

n<=100,允许前导0的子串

(例如132有三个子序列:12 3 132是3的倍数;1 2 13 32则不是)

450

n*n的格子(0~n-1,0~n-1)

你每次跳的距离必须大于等于d

问最少要跳几次才能从(sx,sy)到(tx,ty)

n<=1000 d<=2000 0<=sx,sy,tx,ty<n

800

给你一个长度为n的序列

你可以对这个序列进行任意次操作

每次可以选个x让x(i+1) ^= x(i)

求变换后的最长公共子序列长度的最大值

n<=100 0<=x(i)<=1e18

做法:

225

首先吐槽这个分数...........

看起来是水题无疑了......

3的倍数有特殊性质.......

我直接暴力的...现场赶时间..时间就是分数..懒得写dp...

代码:

#include<set>
#include<map>
#include<list>
#include<queue>
#include<stack>
#include<string>
#include<time.h>
#include<math.h>
#include<memory>
#include<vector>
#include<bitset>
#include<fstream>
#include<stdio.h>
#include<utility>
#include<string.h>
#include<iostream>
#include<stdlib.h>
#include<algorithm>
using namespace std;
int c[55][55];
const int modo=1000000007;
struct MagicNumberThree
{
    int countSubsequences(string s)
    {
        int n=s.length();
        int i;
        static int cnt[3];
        for (i=0;i<n;i++)
        {
            int t=(s[i]-'0')%3;
            cnt[t]++;
        }
        c[0][0]=1;
        int j;
        for (i=1;i<=n;i++)
        {
            c[i][0]=1;
            for (j=1;j<=i;j++)
            {
                c[i][j]=(c[i-1][j-1]+c[i-1][j])%modo;
            }
        }
        int k;
        int ans=0;
        for (i=0;i<=cnt[0];i++)
        {
            for (j=0;j<=cnt[1];j++)
            {
                for (k=0;k<=cnt[2];k++)
                {
                    if ((j+k*2)%3!=0) continue;
                    ans=(ans+(long long)c[cnt[0]][i]*c[cnt[1]][j]%modo*c[cnt[2]][k]%modo)%modo;
                }
            }
        }
        return (ans-1+modo)%modo;
    }
};
#ifdef absi2011
int main()
{
    freopen("input.txt","r",stdin);
    freopen("output.txt","w",stdout);
    
    return 0;
}
#endif

450

继续吐槽分数..

看起来是水题..

然后本来以为答案是1~3,后来找了个答案是4的....

直接玩坏了..

数据:

n=61

d=67

31 60

32 1

大概思路是走到左上角,然后借60 30这个位置跳到右上角,再到32 1这个点

需要4步

现场最后弄了个算法,过了sample和那个数据但是挂System test了

0~2特判

然后把四角和每个边的中点拿出来,再加上起点终点

跑一边bfs

然后挂了这个数据(代码底下测试的数据)

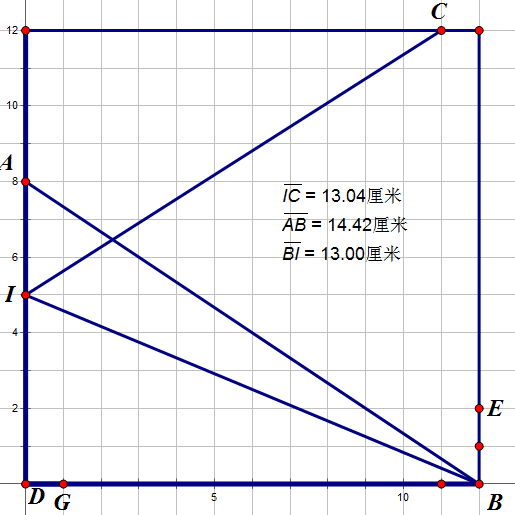
我输出4答案是3..........

然后我怒而hack +9;-3

然后实际做法:

0~2特判

3,4,-1判定方法:把周围一圈和起点终点拿出来跑bfs就行了

#include<set>
#include<map>
#include<list>
#include<queue>
#include<stack>
#include<string>
#include<time.h>
#include<math.h>
#include<memory>
#include<vector>
#include<bitset>
#include<fstream>
#include<stdio.h>
#include<utility>
#include<string.h>
#include<iostream>
#include<stdlib.h>
#include<algorithm>
using namespace std;
inline int dist(int x1,int y1,int x2,int y2)
{
    return (x2-x1)*(x2-x1)+(y2-y1)*(y2-y1);
}
struct point
{
    int x;
    int y;
    point (int xx=0,int yy=0)
    {
        x=xx;
        y=yy;
    }
    int dist(point a)
    {
        return (x-a.x)*(x-a.x)+(y-a.y)*(y-a.y);
    }
};
point b[8005];
int dis[8005];
struct FrogSquare
{
    int minimalJumps(int n, int d, int sx, int sy, int tx, int ty)
    {
        d*=d;
        int i;
        if ((sx==tx)&&(sy==ty)) return 0;
        if (dist(sx,sy,tx,ty)>=d) return 1;
        int j;
        for (i=0;i<n;i++)
        {
            for (j=0;j<n;j++)
            {
                if (dist(sx,sy,i,j)<d) continue;
                if (dist(tx,ty,i,j)<d) continue;
                return 2;
            }
        }
        int num=0;
        b[num++]=point(sx,sy);
        b[num++]=point(tx,ty);
        for (i=0;i<n;i++)
        {
            b[num++]=point(0,i);
            b[num++]=point(n-1,i);
            b[num++]=point(i,0);
            b[num++]=point(i,n-1);
        }
        memset(dis,-1,sizeof(dis));
        dis[0]=0;
        int front=0,rail=1;
        static int que[8005];
        for (;front<rail;front++)
        {
            int now=que[front];
            int i;
            for (i=0;i<num;i++)
            {
                if (dis[i]!=-1) continue;
                if (b[i].dist(b[now])>=d)
                {
                    dis[i]=dis[now]+1;
                    que[rail++]=i;
                }
            }
        }
        return dis[1];
    }
};
#ifdef absi2011
int main()
{
    freopen("input.txt","r",stdin);
    freopen("output.txt","w",stdout);
    FrogSquare x;
    cout<<x.minimalJumps(13, 13, 0, 8, 11, 12)<<endl;
    return 0;
}
#endif

800

其实这个800不比450难

首先,我们可以发现一些性质

我们可以通过这个操作:

(以1 2 4为例)

1 2 4-->1 3 4--> 1 3 7--> 1 2 7 --> 1 2 5

通过1,2,1,2的顺序,我们可以把x(1)给x(3)

同理,我们可以把x(i)给x(j) (i<j)

那么也就是说每个点是前置位所有点的任意xor出来就行

另一方面我们想到之前我们求最长不下降子序列有两种姿势

n^2的dp和n log n的dp

n log n的是dp(i,j)表示到第i个数为止,长度为j的最长不下降子序列的最后一位的最小值是多少

因为每次只修改一个所以我们不需要dp(i,j)

反正就是维护了一个数组

那么我们同样维护一个数组,每次更新

更新的时候可以利用上面的xor抑或方程组的性质

可以找到最优解

(具体看代码?)

#include<set>
#include<map>
#include<list>
#include<queue>
#include<stack>
#include<string>
#include<time.h>
#include<math.h>
#include<memory>
#include<vector>
#include<bitset>
#include<fstream>
#include<stdio.h>
#include<utility>
#include<string.h>
#include<iostream>
#include<stdlib.h>
#include<algorithm>
using namespace std;
long long ans[105];
long long val[65];
struct XorAndLIS
{
    int maximalLength(vector<long long> x)
    {
        int n=x.size();
        int i;
        int cnt=0;
        ans[0]=-1;
        memset(val,-1,sizeof(val));
        memset(ans,-1,sizeof(ans));
        int j;
        ios::sync_with_stdio(false);
        for (i=0;i<n;i++)
        {
            for (j=60;j>=0;j--)
            {
                if ((1ll<<j)&x[i])
                {
                    if (val[j]==-1)
                    {
                        break;
                    }
                    else
                    {
                        x[i]^=val[j];
                    }
                }
            }
            int temp=j;
            for (j--;j>=0;j--)
            {
                if (val[j]==-1) continue;
                if ((1ll<<j)&x[i])
                {
                    x[i]^=val[j];
                }
            }
            for (j=cnt;j>=0;j--)
            {
                long long goal=ans[j]+1;
                long long now=x[i];
                long long now_min=-1;
                int k;
                if (now>=goal)
                {
                    now_min=now;
                }
                for (k=60;k>=0;k--)
                {
                    if (val[k]!=-1)
                    {
                        now^=val[k];
                        if (now>=goal)
                        {
                            if (now_min==-1)
                            {
                                now_min=now;
                            }
                            now_min=min(now_min,now);
                            now^=val[k];
                        }
                    }
                }
                if (now_min>=goal)
                {
                    if ((ans[j+1]==-1)||(ans[j+1]>now_min))
                    {
                        ans[j+1]=now_min;
                    }
                    if (j==cnt) cnt++;
                }
            }
            for (j=0;j<=cnt;j++)
            {
                cout<<ans[j]<<" ";
            }
            cout<<endl;
            if (temp!=-1)
            {
                val[temp]=x[i];
                for (j=60;j>temp;j--)
                {
                    if (val[j]==-1) continue;
                    if (val[j]&(1ll<<temp))
                    {
                        val[j]^=val[temp];
                    }
                }
            }
        }
        return cnt;
    }
};
#ifdef absi2011
int main()
{
    freopen("input.txt","r",stdin);
    freopen("output.txt","w",stdout);
    
    return 0;
}
#endif