题意:

n个数的一个数列(n<=100000)

两个操作

1,区间修改,将[l,r]修改为r

2,询问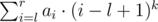的值(0<=k<=5)

做法:

这题似乎和二项式定理有点关系..

[tex](a+b)^k = C_k^0 a^k + C_k^1 a^{k-1}b + ... + C_k^k b^k[/tex]

我们维护区间的值有:

区间a*i^k的和

那么两个区间的合并复杂度就比较高了

我们算一下,右边的值的变化在于系数

系数从i的k次方跳到了i+(mid-l)的k次方

之间的差距就是上面的二项式系数

我们维护下..嗯..

#include<set>
#include<map>
#include<list>
#include<queue>
#include<stack>
#include<string>
#include<math.h>
#include<time.h>
#include<vector>
#include<bitset>
#include<memory>
#include<utility>
#include<fstream>
#include<stdio.h>
#include<sstream>
#include<iostream>
#include<stdlib.h>
#include<string.h>
#include<algorithm>
using namespace std;
int c[100005][6][6];
const int modo=1000000007;
int sum[100005][6];
int val[1<<18][6];
int a[100005];
int tag[1<<18];
inline void updates(int num,int delta)
{
    register int i;
    for (i=0;i<=5;i++)
    {
        val[num][i]=val[num*2+1][i];
        int j;
        for (j=0;j<=i;j++)
        {
            val[num][i]=(val[num][i]+(long long)val[num*2+2][j]*c[delta][i][j])%modo;
        }
    }
}
int sums;
int k;
inline void update(int num,int delta)
{
    register int j;
    for (j=0;j<=k;j++)
    {
        sums=(sums+(long long)val[num][j]*c[delta][k][j])%modo;
    }
}
inline void push_down(int num,int l,int mid,int r)
{
    if (tag[num]==-1) return;
    register int i;
    for (i=0;i<=5;i++)
    {
        val[num*2+1][i]=(long long)sum[mid-l][i]*tag[num]%modo;
        val[num*2+2][i]=(long long)sum[r-mid][i]*tag[num]%modo;
    }
    tag[num*2+1]=tag[num];
    tag[num*2+2]=tag[num];
    tag[num]=-1;
}
inline void build_tree(int num,int l,int r)
{
    tag[num]=-1;
    if (l==r-1)
    {
        register int i;
        for (i=0;i<=5;i++)
        {
            val[num][i]=a[l];
        }
        return;
    }
    int mid=(l+r)/2;
    build_tree(num*2+1,l,mid);
    build_tree(num*2+2,mid,r);
    updates(num,mid-l);
}
inline void change(int num,int l,int r,int l0,int r0,int vals)
{
    if ((l0<=l)&&(r<=r0))
    {
        tag[num]=vals;
        register int i;
        for (i=0;i<=5;i++)
        {
            val[num][i]=(long long)sum[r-l][i]*vals%modo;
        }
        return;
    }
    int mid=(l+r)/2;
    push_down(num,l,mid,r);
    if (l0<mid) change(num*2+1,l,mid,l0,r0,vals);
    if (mid<r0) change(num*2+2,mid,r,l0,r0,vals);
    updates(num,mid-l);
}
inline void query(int num,int l,int r,int l0,int r0)
{
    if ((l0<=l)&&(r<=r0))
    {
        update(num,l-l0);
        return;
    }
    int mid=(l+r)/2;
    push_down(num,l,mid,r);
    if (l0<mid) query(num*2+1,l,mid,l0,r0);
    if (mid<r0) query(num*2+2,mid,r,l0,r0);
}
int main()
{
    #ifdef absi2011
    freopen("input.txt","r",stdin);
    freopen("output.txt","w",stdout);
    #endif
    int i;
    for (i=0;i<=100000;i++)
    {
        int j;
        for (j=0;j<=5;j++)
        {
            int k;
            c[i][j][0]=1;
            for (k=1;k<=j;k++)
            {
                c[i][j][k]=c[i][j-1][k]+c[i][j-1][k-1];
                if (c[i][j][k]>=modo) c[i][j][k]-=modo;
            }
        }
        for (j=0;j<=5;j++)
        {
            int k;
            c[i][j][0]=1;
            int p=1;
            for (k=j;k>=0;k--)
            {
                c[i][j][k]=(long long)c[i][j][k]*p%modo;
                p=(long long)p*i%modo;
            }
        }
    }
    for (i=1;i<=100000;i++)
    {
        int j;
        int p=1;
        for (j=0;j<=5;j++)
        {
            sum[i][j]=sum[i-1][j]+p;
            if (sum[i][j]>=modo) sum[i][j]-=modo;
            p=(long long)p*i%modo;
        }
    }
    int n;
    scanf("%d",&n);
    int q;
    scanf("%d",&q);
    for (i=0;i<n;i++)
    {
        scanf("%d",&a[i]);
    }
    build_tree(0,0,n);
    for (i=0;i<q;i++)
    {
        static char b[15];
        scanf("%s",b);
        int l,r,z;
        scanf("%d%d%d",&l,&r,&z);
        l--;
        if (b[0]=='=')
        {
            change(0,0,n,l,r,z);
        }
        else
        {
            sums=0;
            k=z;
            query(0,0,n,l,r);
            printf("%d\n",sums);
        }
    }
    return 0;
}